How to Forget Jenny's Phone Number
Model Pruning, Distillation, and Quantization: I Read a Bunch of Papers so that You Don't Have to
Note: The ideas presented in this work are not original and solely represent a summary of existing research papers.
Do you also remember how to contact Jenny, your gal from the eighties? I sure do, and rumor has it, her cell has not changed. It’s (sing it with me) ♫ 867-5309 ♪. But unfortunately, our retention of this information is useless to us when performing nearly any task other than embodying Tommy Tutone. As it turns out, our brains are full of useless information like this; brimming with millions of neural pathways largely unused by us in our day-to-day lives.
Machines also experience this phenomenon of excessive information storage. Deep learning models, with their millions (or even billions) of parameters, often contain redundant and unnecessary connections. These connections contribute to the model's large size, slow inference speed, and high memory requirements. To address this issue, researchers have developed techniques known as deep model pruning, distillation, and quantization.
All of these are valuable techniques in the field of deep learning that help address the challenges posed by the increasing complexity and resource demands of modern neural networks. By reducing model size and improving efficiency, these techniques enable the deployment of deep learning models on a wide range of devices, opening up possibilities for real-world applications across various domains.
In this blog post, we will define and explore the principles behind deep model pruning, distillation, and quantization in more detail, and outline the steps of the processes so that you might also apply these techniques. We will delve into the techniques used, the benefits they offer, and the trade-offs involved. So, let's dive in and discover how we can trim the fat and distill the essence of deep learning models to make them more practical and efficient in the real world.
Pruning
Deep model pruning involves identifying and removing unnecessary connections, weights, or even entire neurons from a trained deep learning model. By eliminating these redundant components, the model can become more compact, faster, and more memory-efficient, while still maintaining a high level of accuracy.
Usually, it is advisable to begin with pruning weights only as this does not change the architecture of your model like pruning neurons does. But what exactly does it mean to “prune weights”? This essentially means manually setting the weights of chosen individual parameters in your network to zero. These parameters will then be unable to have an effect on the model’s reasoning. When pruning weights, you want to selectively prune those parameters’ weights that are already near zero, aka, they are already not being of much use. This means that the initial model performance is nearly completely preserved.
We can also think of this in the context of Jenny's number. Pruning weights can be likened to selectively setting certain digits to zero. By doing so, we render these digits insignificant and irrelevant to the interpretation of the phone number, while maintaining the fundamental structure of the phone number. In other words, when pruning weights in Jenny's number, we target the digits whose weights are already near zero- maybe, let’s say, the +1 out front, or the parentheses around the area code. These digits are essentially redundant or provide minimal value to the phone number's meaning. By selectively removing these digits, we streamline the representation of the number and focus on the more crucial and informative digits.

However, simply pruning weights can lead to a sparse model with disconnected neurons, which may result in suboptimal performance during inference1. Sparse models – models where only a small fraction of parameters are non-zero – arise frequently in machine learning. To mitigate this issue, structured pruning can be employed. Structured pruning involves removing entire neurons or groups of neurons instead of individual weights. In the context of our mutual endeavor to forget Jenny's number, structured pruning can be likened to removing certain blocks or segments of digits rather than individual digits. For example, let's say the digits 867 represent one group of neurons, while 5309 represent another group. Structured pruning would involve removing one of these groups of neurons, reducing the overall length of the phone number.

Within the more modern deep convolutional networks, removing neurons can be likened to removing convolutional filters. In these networks, when we prune parameters to make the model smaller, we might not see a substantial decrease in computation time. This is because most of the removed parameters come from the fully connected layers, which are not as computationally intensive as other parts of the network. So, even though we are reducing the size of the model, the computation time doesn't reduce proportionally, and the overall impact on speed might not be as significant as anticipated. Li et al. (2016) gives an example that drives this point home; you may see a case where “fully connected layers occupy 90% of the total parameters but only contribute less than 1% of the overall floating point operations (FLOP)”.
How much do I prune?
When pruning a deep learning model, it is crucial to strike a balance between model size reduction and preserving accuracy. Pruning too aggressively can result in significant accuracy degradation (let’s forget all phone numbers to forget Jenny’s!), while pruning conservatively may not yield substantial benefits in terms of model compression (let’s just forget the number 7 in her number). Therefore, various pruning algorithms and heuristics have been developed to guide the pruning process and find the optimal trade-off between size and performance.
Early Suggestions
The pioneering work by Le Cun et al. (1989) introduced the concept of "Optimal Brain Damage," which laid the foundation for weight pruning in neural networks. The Optimal Brain Damage method identifies and prunes weights using a theoretically justified saliency measure.
Building upon this early work, Hassibi et al. (1993) proposed the "Optimal Brain Surgeon" method, which takes the pruning concept a step further. The Optimal Brain Surgeon method utilizes second-order derivative information to determine the importance of weights. By analyzing the curvature of the loss surface with respect to the weights, the method identifies and removes unimportant weights more accurately than purely relying on first-order gradient information. This approach helps to retain more critical connections while further reducing model complexity.
Both the Optimal Brain Damage and Optimal Brain Surgeon methods have significantly contributed to the field of neural network pruning, inspiring subsequent research on weight pruning techniques. These methods demonstrated the potential of pruning as a powerful means to compress neural networks without sacrificing performance. While the field has since evolved with the introduction of various other pruning criteria and techniques, the early work of Le Cun et al. and Hassibi et al. remains foundational in exploring methods to efficiently and effectively remove unimportant weights from neural networks.
Norms
Pruning based on the L2 norm of the neuron's weights is a commonly used technique. The L2 norm, also known as the Euclidean norm or the Frobenius norm, measures the "length" of a vector. Thus, the L2 norm of a neuron's weight refers to the magnitude of the weight. Neurons with smaller L2 norm values are considered less influential to the network’s overall performance, so pruning in this way nearly completely preserves the model’s initial performance.
You’ve heard of L2? Get ready for L1. The L1 norm, also known as the Manhattan norm or the taxicab norm, is another way to prune. Geometrically, the L1 norm measures the distance between the origin and the vector's endpoint when following only horizontal and vertical paths, resembling the movement of a taxicab in a city grid, hence the name "taxicab norm." L1 regularization is specifically used to prevent overfitting. In linear regression, for example, L1 regularization adds a penalty term to the loss function proportional to the L1 norm of the model's weights. This encourages some of the weights to become exactly zero, effectively selecting a subset of the most relevant features and leading to a more interpretable and compact model.
You’ve heard of L1? Get ready for L0. The L0 norm is less commonly used than the L1 and L2 norms, because it is a bit more complex. Unlike the L1 norm (sum of absolute values) and L2 norm (Euclidean norm, sum of squared values), the L0 norm counts the number of non-zero elements in a vector. In other words, it measures the "sparsity" of a vector by counting the number of non-zero components. L0 norm regularization has been explored as a technique to promote sparsity in models. Unlike L1 regularization, which encourages small individual weights, and L2 regularization, which encourages small overall weight magnitudes, L0 regularization explicitly penalizes the number of non-zero weights in a model.
The L0 norm is more complex than the L1 and L2 norms because of its non-convex nature and lack of gradients, which make optimization challenging. Computing the L0 norm involves counting the number of non-zero elements in a vector, leading to a combinatorial problem that becomes increasingly difficult as the vector dimensionality grows. Furthermore, the non-convexity of the L0 regularization term introduces multiple local minima, making it difficult to find the global minimum during optimization. Additionally, the L0 norm lacks gradients almost everywhere, rendering traditional gradient-based optimization methods impractical. While inducing sparsity is an appealing objective, L1 regularization (Lasso) effectively achieves similar results by encouraging many weights to become exactly zero, making it a more computationally tractable and widely used alternative to the L0 norm.
You’ve heard of L0? Get ready for L-1. Just kidding. Moving on.
Pruning weights using norms in neural networks is analogous to selectively forgetting or removing certain digits from Jenny's phone number based on their importance. Just as we might prioritize specific digits in Jenny's phone number that are more critical for identification, pruning techniques focus on identifying and retaining the most relevant connections (weights) in the network.
When using norms for pruning, such as L0, L1, or L2 norms, the magnitude of each weight is evaluated to determine its significance in the model's performance. For example, applying norm pruning might involve reducing the importance of specific digits in Jenny's phone number, like reducing the significance of the "8" and "6" digits to make them smaller or even zero.
Data-Driven Pruning
Another commonly used technique, slightly more advanced than magnitude cutoff, is data-driven pruning. This is a technique that leverages the activation patterns of neurons during the training process to identify and remove redundant or less informative connections or neurons. When the model is training, it will look for two main things in the activation patterns: (1) neurons that activate in a very similar manner and also have very similar outputs, and (2) neurons that output near-zero values. The first weights are pruned as they likely represent duplicate parameters, meaning they can be considered overlapping in terms of their functionality within the network. It is possible that they are capturing redundant information or encoding similar features- and we don’t need both! An added benefit to this technique is that because pruning such neurons now allows our model to prevent over-representation of similar information, we can avoid potentially overfitting to the training data and improve generalization capabilities.
Pruning based on activation patterns can be compared to forgetting or disregarding certain patterns or combinations of digits in Jenny's phone number. Activation-based pruning takes into account the relevance of neurons' activations and their impact on the network's functionality. Similarly, we can forget or prune certain patterns in the phone number that do not significantly contribute to its meaning or purpose. For instance, there’s a consecutive 6-7 that might help you remember the number. So a fairly safe way of saving brain space is to ✨forget that✨.
Taylor Expansions
Recently, researchers have come out with a bold, new assertion:
Many pruning methods rely on the belief that the magnitude of a weight and its importance are strongly correlated. We question this belief and observe a significant gap in correlation between weight-based pruning decisions and empirically optimal one-step decisions – a gap which our greedy criterion aims to fill.
In that paper, Molchanov et al., (2019) presented a novel method for identifying and pruning neurons (filters) in neural networks based on their contributions to the final loss. The key idea is to estimate the importance of each neuron and iteratively remove those with smaller scores, effectively pruning the network while preserving its overall performance. But instead of using weight magnitudes, the paper defines the importance as “the squared change in loss induced by removing a specific filter from the network”. But to avoid costs, this is not computed exactly; instead, it is approximated with a Taylor expansion, “resulting in a criterion computed from parameter gradients readily available during standard training”. The paper explored two variations of this method, each using different approaches to approximate a filter's contribution.
The first variation involves using the first-order Taylor expansion to estimate a filter's contribution to the loss function. By considering the gradient of the loss with respect to the filter's activations, we can approximate its influence on the overall loss. Neurons with smaller contributions are pruned, resulting in a sparser network architecture.
The second variation leverages the second-order Taylor expansion, a more refined approximation, to evaluate a filter's significance. By considering both the gradient and the curvature of the loss with respect to the filter's activations, we obtain a more accurate estimate of its impact on the final loss. Again, neurons with lower scores are pruned iteratively.
Through extensive experiments and comparisons, the paper demonstrated the effectiveness of this method in producing pruned networks that retain high performance while reducing computational and memory requirements, paving the way for more resource-efficient and streamlined deep learning models.
Using this method on your own brain would find that- hey- Jenny’s phone number neuron actually doesn’t seem to be used when performing a lot of your day-to-day tasks, and get rid of it for you.
LDA
LDA, which stands for Linear Discriminant Analysis, is a statistical method used for dimensionality reduction and classification tasks. While LDA itself is not typically used as a pruning criterion in neural network pruning, it has relevance in certain contexts.
In traditional machine learning, LDA is a supervised learning algorithm used for dimensionality reduction to find the linear combination of features that maximizes the separation between different classes in the data. It projects the data onto a lower-dimensional subspace while preserving the class-discriminative information.
In some works, researchers have explored the combination of LDA with neural network pruning. The idea is to use LDA as an additional criterion to identify less important neurons or connections in the network. By leveraging the class-discriminative information from LDA, it is possible to guide the pruning process to retain neurons that are more relevant for the specific classification task at hand.
In this context, LDA can be considered a supplementary pruning criterion, used in conjunction with other criteria such as weight magnitudes, sensitivities, or regularization terms. By combining LDA with these criteria, researchers aim to produce pruned models that are not only more efficient but also more focused on the class-discriminative features, potentially leading to improved performance on the classification task.
It's essential to note that the use of LDA as a pruning criterion in neural networks is not as widespread as other more established criteria, such as weight magnitude-based pruning or L1 regularization. The effectiveness of LDA as a pruning criterion may depend on the specific dataset and classification problem, and it is an area of ongoing research in the intersection of neural network pruning and traditional machine learning techniques.
I know there’s at least one guy out there that is a big proponent of LDA-based pruning. He’s seen a lot of positive results (Tian et al., 2017, Tian et al., 2018), but then again, the topic was also his PhD thesis (Tian 2020).
Cosine Distance
Cosine distance, also known as cosine similarity, is a similarity metric used to measure the cosine of the angle between two non-zero vectors. In weight pruning it is used to assess the similarity between weight vectors in the model. Neurons with weight vectors that are more similar to each other have a smaller cosine distance, indicating that their contributions to the model may be redundant. By setting connections with smaller cosine distances to zero, the pruning process aims to reduce redundancy and achieve a more efficient and compact network architecture.
Cosine distance pruning takes into account the direction of weight vectors rather than their magnitudes. This characteristic makes it particularly useful in situations where the magnitudes of weights may vary significantly but the directionality is essential for capturing meaningful patterns in the data.
Moreover, cosine distance pruning can be seen as a measure of orthogonality between weight vectors. When two weight vectors are highly orthogonal (cosine distance close to 1), they are likely to capture different patterns in the data, making their combined contributions valuable. On the other hand, when two weight vectors are nearly collinear (cosine distance close to 0), they may capture similar information redundantly, and pruning one of them can lead to increased model efficiency without significantly sacrificing performance.
You could think of it this way: you store a lot of phone numbers in your head. Those synapses have direction, ie, they go somewhere next. Most of the phone numbers in your head would probably point you next in the direction of calling someone. However, Jenny’s number probably wouldn’t; more likely it would point you in the direction of singing. This method would therefore find a higher cosine distance value for Jenny's number, indicating that its synapses have a dissimilar direction compared to the general trend of the other phone numbers stored in your head. This suggests that Jenny's number might actually be important. So, this is maybe a bad method for our current purposes.
Entropy
Entropy is a concept from information theory that quantifies the uncertainty or randomness of a probability distribution. However it has been explored as a pruning criterion also. You can think of the value entropy as being how much diverse information a synapse or neuron contains, with more information corresponding to a higher entropy value.
In weight pruning, entropy is used to measure the uncertainty in the distribution of weights for each neuron or connection. Neurons with weight distributions that are more uncertain or spread out have higher entropy values, indicating that their contributions to the model may be less informative or redundant. By setting connections with higher entropy values to zero, the pruning process aims to remove less informative connections and achieve a more efficient and compact network architecture.
If you were to apply the concept of entropy to prune your brain's storage of phone numbers, you would indeed prioritize and retain the more important and frequently used phone numbers of people who really exist. Entropy, in this context, would help you identify the distribution of phone numbers in your memory, taking into account their frequencies and relevance. For instance, real phone numbers of people you frequently interact with and use for communication would likely have higher occurrences and contribute to a more predictable pattern in the phone number distribution. As a result, their entropy values would be lower, indicating a more uniform and less uncertain distribution.
On the other hand, fictional phone numbers, such as Jenny's number, would be less frequent and contribute to a more diverse and uncertain distribution, leading to a higher entropy value. By applying entropy-based pruning to your brain's phone number storage, you would be more likely to retain the real and important phone numbers with lower entropy values, as they form a consistent and predictable pattern in your memory. Meanwhile, the fictional and less frequently used phone numbers with higher entropy values, like Jenny's number, may be pruned or removed as they contribute less to the overall representation of phone numbers that are relevant to your daily life and communication.
Entropy-based pruning takes into account the diversity of weights rather than solely relying on their magnitudes or directions. This characteristic makes it particularly useful in situations where the model may have multiple solutions with different weight distributions that achieve similar performance.
Correlation Matrices
The correlation matrix, a matrix showing correlation coefficients between variables, can be employed as a pruning criterion in the context of neural network pruning. To utilize the correlation matrix for pruning, weights or neuron activations from specific layers are collected. A correlation matrix is then computed to analyze the relationships between these weights or neurons. Strong positive correlations indicate redundant connections or neurons that tend to change together, making them suitable candidates for pruning to reduce redundancy. Conversely, strong negative correlations imply that certain connections or neurons change in opposite directions, suggesting that they might provide complementary information. Such connections or neurons may be retained to preserve network diversity. By incorporating the correlation matrix as a pruning criterion, neural networks can be made more efficient and compact by removing redundancies and retaining valuable connections or neurons. However, the effectiveness of the correlation matrix as a pruning criterion depends on the architecture, dataset, and task, necessitating careful experimentation and evaluation to optimize model efficiency and performance.
Correlation matrices measure the correlation coefficients between different variables, which, in this context, would represent the patterns or relationships between various phone numbers in your brain's memory. Real phone numbers of people you frequently interact with and use for communication would likely have stronger correlations with each other, reflecting a more interconnected and related network of phone numbers. On the other hand, fictional phone numbers like Jenny's, which are unrelated to your real-world experiences, might have weaker correlations with other real phone numbers, indicating a less significant relationship between them. This means that Jenny’s number would be seen as useful information and not be pruned.
A Conclusion
So within that discussion there were a few convoluted pruning methods. I think here, then, it is generally considered wise to reflect upon some words of a dusty 14th-century English philosopher, as many do when chewing on such information. Let’s revisit Occam’s Razor:
The simplest explanation is usually the best one.
Great, but how does this idea hold up to 21st-century testing? Well, at least one group found that
Across thousands of experiments, we demonstrate that complex techniques (Molchanov et al., 2017; Louizos et al., 2017b) shown to yield high compression rates on smaller datasets perform inconsistently, and that simple magnitude pruning approaches achieve comparable or better results. Based on insights from our experiments, we achieve a new state-of-the-art sparsity-accuracy trade-off… using only magnitude pruning.
Some of our methods did not work on eliminating Jenny’s number, but rather, encouraged us to keep it. This is a great lesson in: not every tactic we discuss in this blog post will work for what you are specifically trying to achieve. You must make an informed decision before losing information based on your goals and expectations for your model.
Cool, But When Do I Prune My Model?
Pruning techniques can be applied anywhere: as a first step, during the training process or as a post-training optimization step. Let’s forget about Jenny for a moment to lay out the options, and revisit this question at the end of this section.
Pruning After Training:
The standard time to prune if you are using a weight magnitude-based pruning approach is after training. This is the classic approach to pruning: the train-prune-fine-tune cycle. Let’s explore this idea first.
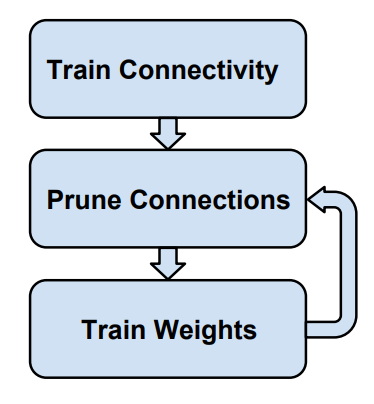
Train-Prune-Fine-tune
The core idea behind this strategy is to train the model once to learn which neural connections are actually important, prune those that aren’t (are low-weight) and then train again to learn the final values of the weights.
Once you have trained your model for the first time, you may remove connections with weights below a certain threshold. Because the model has already undergone training, during the fine-tune phase, you have the option to start training from scratch again or reuse the corresponding weights from the initial training phase. Studies have shown that reusing the initial weights is typically better (and not to mention, faster) (Han et al., 2015). This is most likely because in Convolutional Neural Networks (CNNs), learned patterns or representations become highly dependent on the presence of other specific features. When certain features are learned in a way that they rely on the existence of other features, they become “fragile”, and any disruption to these co-adapted relationships can negatively impact the network's performance. Researchers have found that gradient descent, the optimization algorithm used to train neural networks, is generally successful in finding good solutions during the initial training phase. However, if some layers of the network are re-initialized and then retrained, it becomes challenging for the network to rediscover the same set of fragile co-adapted features, leading to a loss of performance compared to the original trained network (Yosinski et al., 2014).
This process in and of itself has the benefit that it can also lead to efficient structured pruning too. If you’ve set several connections to zero, then there may be neurons with neither inputs nor outputs. If this is the case, then the entire neuron and its connections can be removed completely. Although, added benefit here: you don’t have to do it manually. Zeroed out gradients result in zeroed out weights and vice-versa. When a neuron has no input synapses, it cannot have any effect on the loss, causing the gradient for its output synapse to be zero. Similarly, if a neuron dead-ends, its input synapse gradient becomes zero. Regularization will then zero out the weight of the synapse too, and then all is gone without you having to say anything (Han et al., 2015).
This is all good and well, but typically learning the connections of importance, like anything in ML, is an iterative process. You could take this idea one step further by iteratively repeating the pruning and retraining steps. Then the network can converge to a configuration with the minimum number of connections necessary for its task.
→Train-Prune-Fine-tune→
A similar method is to fully retrain the pruned network instead of simply fine-tuning it. Fine-tuning is performed at the lowest learning-rate to ensure that the pre-trained knowledge captured in the initial layers of the neural network is preserved while adapting the later layers to the new task or dataset2. However, retraining would use the same learning-rate as the initial train. There are two general ways in which this is done:
Weight Rewinding and
Learning-Rate Rewinding
Weight rewinding involves reverting the model's weights back to a previous state during the training process (Frankle et al., 2019), typically to a point where the model achieved better performance. During fine-tuning, the model's performance on a validation set is monitored over several epochs. At a certain point, if the model's performance starts to degrade or stagnate, the training process is paused. Once the training is paused, the model's weights are reset back to a previous state, typically to the point where it achieved better performance during the fine-tuning process. After rewinding the weights, the fine-tuning process is resumed from the previous state. The training continues as usual, allowing the model to explore different solutions while leveraging the previously learned representations. The weight-rewinding process can be repeated multiple times during fine-tuning. After each rewind, the model may find new and better solutions, leading to improved performance on the target task. This technique has been shown to improve fine-tuning outcomes and can be particularly useful when working with limited data or complex tasks where fine-tuning alone might not yield satisfactory results.
But, despite its name, weight rewinding actually rewinds both the weights and the learning rate. What happens if you only rewind the learning rate (Renda et al., 2020)? The learning rate schedule during training is periodically reset to a previously lower value, again, to where the model's performance was better. Initially, the neural network is trained on a large dataset using a specific learning rate schedule. This schedule may involve gradually decreasing the learning rate over epochs to facilitate convergence. Similarly to weight rewinding, the validation set performance is monitored and pauses when it stagnates. When the training progress slows down, the learning rate is reset to a previously lower value, usually from a checkpoint where the model showed better validation performance. After rewinding the learning rate, the training process resumes from the previous state, allowing the model to continue training with the adjusted learning rate. Again, this can be repeated multiple times. The key idea behind learning rate rewinding is to counteract potential issues like getting stuck in local minima or slow convergence during training. By occasionally resetting the learning rate to a point where the model made better progress, the technique allows the model to explore different regions of the optimization landscape and potentially escape suboptimal solutions. This has been shown to be beneficial in situations where the learning rate schedule might not be optimal for the entire training process or when the optimization landscape is challenging.

Both rewinding techniques outperform fine-tuning, forming the basis of a network-agnostic pruning algorithm that matches the accuracy and compression ratios of several more network-specific state-of-the-art techniques. However, some studies have also shown that learning rate rewinding matches or outperforms weight rewinding in many scenarios (Renda et al., 2020).
Pruning During Training:
In this approach, compared to pruning after training, connections are dynamically deactivated during training based on their importance, but now, weights are allowed to adapt and potentially reactivate. Pruning while training can lead to a more efficient model since unnecessary connections are pruned early, potentially reducing memory and computation requirements during training. However, it requires careful handling to avoid abrupt changes in the network's structure and the risk of over-pruning, which can hurt performance. There are a few ways in which this is done.
Sparse Training
Instead of simply shutting off connections permanently during the training session, another technique is to allow the weights to reactivate based on gradient updates (Zhu & Gupta 2017). If the gradients indicate that a deactivated connection is becoming important for the task at hand, it can gradually regain its weight and become active again. This method is known as "sparse training" or "dynamic sparsity." It is a form of weight pruning that introduces a dynamic element to the pruning process, and has been shown to be more efficient than the iterative pruning and re-training static approach used by Han et al. (2015) (Liang et al., 2021) .
In traditional weight pruning, connections with low weights are directly removed from the neural network, making them permanently inactive for the rest of the training process. While this can lead to a more compact model, it can also be quite aggressive, potentially causing abrupt changes in the network's structure and learned representations. This aggressive pruning may also hinder the network's ability to recover from pruning-induced performance drops. In contrast, sparse training takes a more gradual and adaptive approach. During the training process, instead of permanently removing connections, the weights of less important connections are allowed to be very close to zero, effectively "deactivating" those connections. However, these deactivated connections are not entirely removed from the network; they are still present and can be potentially reactivated.
By allowing the weights to reactivate, sparse training strikes a better balance between model size and performance. It enables the network to retain more flexibility during the training process and can often result in improved convergence and higher accuracy compared to traditional static pruning techniques. Additionally, dynamic sparsity can mitigate the potential negative impact of aggressive pruning and provide more robustness to pruning-induced changes in the network's architecture.
Gradual Random Connection/Neuron Removal
Another strategy is traditional dropout, where during training, random neurons are "dropped out" or set to zero with a certain probability. This dropout process acts as a regularization technique, preventing neurons from co-adapting and thus improving the generalization of the model. However, dropout was initially seen as a heuristic with no formal Bayesian interpretation.
To turn this around, a supposed reinterpretation of dropout , “Variational Dropout”, was introduced. The concept was proposed by Kingma et al. in their paper "Variational Dropout and the Local Reparameterization Trick" (Kingma et al., 2015). Variational Dropout provides a Bayesian justification for dropout by casting it as a probabilistic model. It interprets dropout as approximating an inference process in a Bayesian neural network, where the dropout masks can be seen as random variables that follow a Bernoulli distribution.
One of the significant extensions facilitated by Variational Dropout is the use of learnable dropout rates. In traditional dropout, the dropout rate (the probability of dropping out a neuron) is usually fixed and set beforehand. However, with Variational Dropout, the dropout rates themselves become learnable parameters. This means that the neural network can now adaptively adjust the dropout rates during training, allowing the model to determine the most suitable dropout probabilities for different layers or neurons based on the data and task at hand.
Variational Dropout unlocks the potential for more flexible and adaptive dropout strategies. This allows the model to better explore the trade-off between regularization and expressive power, leading to improved performance and generalization on various tasks.
The work by Molchanov et al. (2017) demonstrated an intriguing discovery in the context of Variational Dropout and per-parameter dropout rates. Molchanov and his team proposed a post-processing step where weights with high dropout rates (i.e., those that are less relevant for the learned task) are removed or pruned from the model resulting in highly sparse solutions (Gale et al., 2019). Furthermore, this technique is capable of representing a lower-bound of the accuracy-sparsity trade-off curve. What do I mean by this?
The accuracy-sparsity trade-off refers to the relationship between the level of model sparsity (the proportion of pruned weights or connections) and the resulting model's accuracy. As models become sparser (i.e., more weights are pruned), their size and computational requirements decrease, but there is typically a trade-off with accuracy, as important information might be lost. By varying the dropout rates for different weights, Variational Dropout can effectively sample different sparsity levels and corresponding accuracies during training. The model becomes capable of finding solutions along the accuracy-sparsity trade-off curve, ranging from dense models with high accuracy to highly sparse models with reduced accuracy. Because it allows the model to probe different points along the accuracy-sparsity trade-off curve, it effectively represents a lower-bound of the curve.
The “Lottery Ticket Hypothesis”
While sparsity is traditionally thought of as a model compression technique, independent studies have recently suggested that the value of sparsification in neural networks is misunderstood, and that once a sparse topology is learned it can be trained from scratch to the full performance achieved when sparsification was performed jointly with optimization.
The "Lottery Ticket Hypothesis" is a concept that suggests that within large, over-parameterized neural networks, there exist small subnetworks or "winning tickets" that, when trained in isolation, can achieve high performance on a given task. These winning tickets are essentially sparse, low-complexity subnetworks, and they are called "lottery tickets" because finding them is akin to winning a lottery.
The Lottery Ticket Hypothesis was introduced by Frankle & Carbin (2018) in their paper titled "The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks." Their research aimed to explore the behavior of neural networks during the training process and to investigate whether certain subnetworks within these networks have inherent properties that lead to high performance when trained from scratch.
The key findings of the Lottery Ticket Hypothesis are as follows:
Existence of Winning Tickets: Within the initial, randomly initialized weights of a large neural network, there exist small subnetworks (winning tickets) that can achieve high accuracy on the target task when trained in isolation, even without relying on the rest of the network.
Significance of Initialization: The discovery of these winning tickets is highly sensitive to the specific weight initialization used during the training process. The initial weights of the network play a crucial role in determining whether these winning tickets exist or not.
Pruning and Reinitialization: To identify winning tickets, the researchers employed the iterative magnitude pruning technique (which we discussed), where they iteratively pruned unimportant weights and then reinitialized the pruned network. Surprisingly, the same winning tickets were found across different pruning iterations, indicating that the winning tickets were relatively stable structures.
Training Iterations Matter: Winning tickets do not emerge instantly during the early stages of training. They typically appear only after multiple training iterations, and they can be challenging to find without extensive search methods.
The Lottery Ticket Hypothesis suggests that instead of training large networks and applying pruning techniques to achieve sparsity, it might be more efficient to find these winning tickets early on and train them in isolation. Subsequent training can be carried out with full sparsity, leveraging sparse linear algebra techniques to significantly speed up the time it takes to find a solution (Gale et al., 2019).
Interesting turn of events here. In 2019, Gale et al. conducted various experiments comparing two different approaches: training a neural network from scratch using a learned sparse architecture versus incorporating sparsification as part of the optimization process.
Learned Sparse Architecture: In the first approach, the authors trained a neural network from scratch, where they initialized the architecture with a predefined sparse structure. During training, the network learned the weights for the remaining connections.
Sparsification as Part of Optimization: In the second approach, the authors incorporated sparsification directly into the optimization process. They employed pruning techniques during training, iteratively removing unimportant weights and retraining the network. This allowed the model to progressively discover and retain only the most important connections, leading to a sparse representation.
The key finding was that the second approach, where sparsification was integrated into the optimization process, consistently outperformed the first approach, where the network was trained from scratch with a learned sparse architecture. There are a two main reasons why the second approach may have outperformed the first:
Adaptive Sparsity: Sparsification during the optimization process allowed the model to adaptively determine the optimal sparsity level based on the specific task and data. This adaptability allowed the model to fine-tune the level of sparsity to retain crucial information while reducing unnecessary complexity.
Gradient Information: When sparsification is part of the optimization process, the model has access to gradient information, enabling it to better adjust and fine-tune the remaining weights after pruning. This information is valuable in maintaining the model's performance even with a reduced number of parameters.
Overall, the experiments conducted in the paper showed that incorporating sparsification directly into the optimization process leads to more effective and efficient model training, resulting in better performance compared to training from scratch using a learned sparse architecture. This finding emphasizes the importance of integrating pruning techniques into the training process to achieve superior performance and discover more effective sparse neural network representations.
Cool! But anyways, moving on.
Mask Learning
Mask learning is a pruning technique that involves training a neural network to learn a binary mask that selectively prunes or retains certain connections or weights during the training process. The process of mask learning can be summarized as follows:
Mask Initialization: At the beginning of training, a binary mask is initialized with ones, indicating that all connections in the network are active.
Joint Training: During the training process, the network is trained jointly with the binary mask. The mask is updated along with the model's weights during each iteration of the optimization process.
Mask Update Rule: The mask update rule determines how the binary mask is adjusted based on the learned weights. The update rule can be designed to promote sparsity by setting certain weights to zero, effectively pruning the corresponding connections.
Mask Regularization: To encourage the mask to maintain sparsity, mask regularization techniques can be applied during training. Mask regularization penalizes non-sparse masks, incentivizing the network to learn a more sparse representation.
Fine-tuning (Optional): After the initial training, fine-tuning can be performed with the pruned connections to allow the model to recover from any potential drops in performance.
The specialized agents trained alongside the main neural network in this process are responsible for learning binary masks that selectively prune or retain filters of certain layers.
Various approaches have been explored to train these pruning agents effectively. One approach involves inserting attention-based layers, where the agents use attention mechanisms to focus on the most informative filters for the given task. These attention-based mechanisms allow the agents to learn to emphasize important filters while neglecting less relevant ones, resulting in more targeted pruning decisions.
Another method to train pruning agents is through reinforcement learning. In this approach, the agents are treated as reinforcement learning agents, and they receive rewards based on the impact of their pruning decisions on the network's accuracy. By maximizing the reward signal, the agents learn to make more informed pruning choices that lead to improved performance.
This technique has been shown to achieve effective model compression with minimal loss in performance.
At this point, if you are like me, you’re wondering the real difference between masked learning and Variational Dropout. I’ll tell you:
Model Efficiency: Masked learning can be more computationally efficient than variational dropout, especially in large models. Variational dropout involves sampling from dropout rates as a distribution, which introduces additional overhead during training due to the randomness. On the other hand, masked learning involves straightforward binary masks that can be efficiently applied during forward and backward passes.
Interpretability: Masked learning can lead to more interpretable models. By learning binary masks, you can directly observe which connections or units are active and contributing to the model's decision-making process. This transparency can be valuable for understanding the model's behavior and debugging potential issues.
Task-specific Constraints: If the task at hand has specific constraints or requirements on the model architecture, masked learning can be a more suitable choice. For instance, in some scenarios, it might be necessary to enforce sparsity in certain parts of the network, which can be achieved using masks.
Penalty-based Pruning
Penalty-based methods are a class of pruning techniques used to achieve model compression by imposing penalties or regularization terms on the neural network's weights during the training process. These penalties encourage the network to adopt a more sparse representation by driving certain weights to zero or close to zero, effectively pruning connections.
There are several penalty-based methods commonly used for pruning:
L1 Regularization (Lasso): L1 regularization adds a penalty term to the loss function proportional to the absolute values of the weights. This encourages sparsity since it tends to drive many weights to exactly zero. As a result, unimportant connections are effectively pruned, leading to a more compact model.
L0 Regularization: Unlike other common regularization techniques such as L1 (Lasso) and L2 (Ridge) regularization, which penalize the magnitude of the weights, L0 regularization directly targets the number of non-zero weights.
Group Lasso: Group Lasso extends L1 regularization to enforce sparsity at the group level. It groups weights together (e.g., filters in convolutional layers) and applies the L1 penalty to each group as a whole. This ensures that entire groups of weights can be pruned together, leading to structured and more interpretable pruning.
Elastic Net: Elastic Net combines L1 and L2 (Ridge) regularization, which results in a penalty term that encourages both sparsity and weight shrinkage. The combination of the two penalties provides a balance between individual weight pruning and overall weight regularization.
Sparse Group Lasso: This method combines Group Lasso and L1 regularization, enabling pruning at both the individual weight and group levels. It is particularly effective in structured pruning, where entire groups of connections can be removed.
Adaptive Sparsity Methods: These methods introduce learnable sparsity parameters during training. By optimizing these parameters, the network can dynamically control the sparsity level, allowing it to balance performance and model size more effectively.
Dropout as a Regularizer: Although dropout is commonly used as a regularization technique during training to prevent overfitting, it can also be seen as a penalty-based method. During training, dropout randomly sets some weights to zero, effectively introducing a form of regularization that encourages a more robust and sparse model.
Penalty-based methods are popular for their simplicity and effectiveness in inducing sparsity. By adding appropriate regularization terms to the loss function, these methods naturally encourage weight pruning and allow the model to adaptively adjust its structure based on the training data and task requirements. As a result, penalty-based pruning techniques have been widely adopted for model compression, enabling more efficient and resource-friendly deep learning models.
Pruning Before Training:
Although perhaps slightly unintuitive at first, pruning before training, also known as network initialization pruning, is also a possibility. At the beginning, the neural network is created with a predefined architecture and randomly initialized weights. This forms the starting point for the pruning process. Based on certain criteria or heuristics, specific connections or weights are identified for pruning. The criteria might include weight magnitudes, sensitivities, or any other measure of importance. Connections that meet the pruning criteria are removed, resulting in a sparser network architecture. But, what are these criteria, exactly? We haven’t begun to train the model yet, so how do we know which connections are unimportant?
Well, there is no way to really know, is the answer. So generally a random pruning approach is used at the initialization stage. Randomly selected connections are pruned, and this process is repeated multiple times to create a variety of sparse network architectures. The idea behind this is, if you prune in a variety of ways before training, you may have just been able to skip the process of finding lottery tickets and by chance have started with one. This sounds not so intelligent. Let me tell you what the community, as of this year, has to say about that:
It has been observed in practice that applying pruning-at-initialization methods to neural networks and training the sparsified networks can not only retain the testing performance of the original dense models, but also sometimes even slightly boost the generalization performance. Theoretical understanding for such experimental observations are yet to be developed.
That’s what I thought. Nevertheless, pruning fractions below a certain threshold have been shown to allow gradient descent to drive training loss to near-zero while maintaining good generalization performance. Perhaps even more surprisingly than this is that as the pruning fraction increases, Yang et al. (2023) finds that the generalization bound improves, challenging the traditional trade-off between model complexity and generalization. These findings suggest that carefully pruned neural networks can achieve both efficient training and better generalization, offering promising insights for building more resource-efficient models. However, the optimal pruning fraction may vary across datasets and network architectures, and further research is ongoing to fully understand and leverage the benefits of pruning in deep learning.
So, take that as you will!
That Was Too Much Information. So Again… When Do I Prune?
Of course, whether to prune while training or after training depends on the specific pruning technique and your goals for model compression and performance. Let’s summarize the possibilities as a good wrap up:
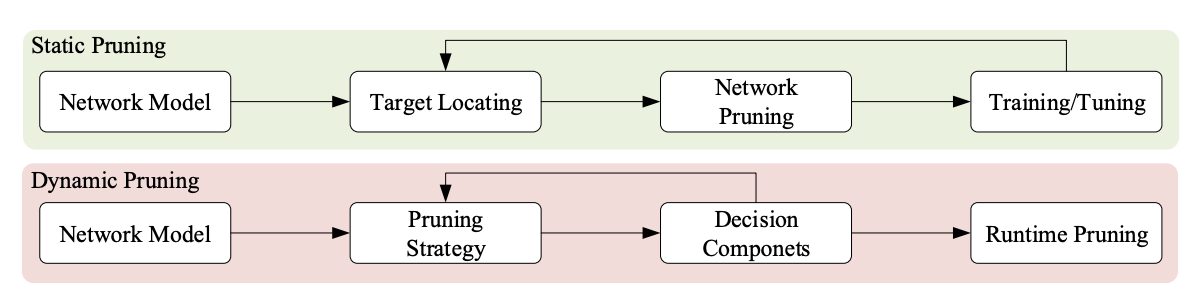
Pruning After Training (Static Sparsity): Pruning after the initial training phase involves removing connections or filters from the trained model in a separate post-processing step. This allows the model to fully converge during training without any interruptions, ensuring that the learned representations are well-established. After pruning, the model can be further fine-tuned to recover from any potential performance drop caused by the pruning process. Pruning after training is generally more stable and less likely to cause overfitting. It can be useful when you want to fine-tune a pre-trained model for a specific task or when you prefer a more controlled approach to pruning.
Pruning During Training (Dynamic Sparsity): In this approach, pruning is integrated into the optimization process as an additional regularization technique. During training iterations, less important connections are dynamically removed or pruned based on certain criteria or heuristics. This allows the model to explore different levels of sparsity and adapt its architecture throughout the training process. Dynamic sparsity can lead to more efficient models since unimportant connections are pruned early, potentially reducing memory and computation requirements. However, it requires careful handling to avoid abrupt changes in the network's structure and the risk of over-pruning, which can hurt performance.
Pruning Before Training (Pre-training Pruning): Pre-training pruning, as the name suggests, involves pruning certain connections or weights from the neural network before the training process begins. The advantage lies in potentially faster training, as the initial model size is reduced, and the network can converge more quickly. However, it requires careful selection of pruning criteria to avoid removing important connections too aggressively.
In some cases, hybrid approaches can be used. This allows you to achieve a balance between early model compression and ensuring a fully converged model. But really, all approaches have their merits and may be suitable depending on the task, dataset, and resource constraints. Proper experimentation and understanding of the trade-offs are crucial to selecting the most effective time to prune.
Pruning techniques, whether applied as a first step, during the training process, or as a post-training optimization step, can have different effects on our memory of Jenny's phone number "867-5309." Let's then return to our question (how to forget her number) and put all of this new knowledge to the test to choose with formulation is best for our specific problem statement:
Pruning as a First Step: If we prune our brains at the initial stage, it means we are selective from the very beginning about what information we store, including phone numbers. In this case, we might choose to exclude fictional phone numbers like Jenny's from the outset, as they may not be considered crucial for our daily communication needs. As a result, Jenny's number might not even be stored in our memory in the first place, as it was pruned early on due to its fictional nature.
Pruning During the Training Process: During the training process (as we grow up and gather information), our brain continuously prunes and adjusts the connections and information it retains based on our experiences and the frequency of use. If we encounter Jenny's number during the training process but rarely use or interact with it, our brain might prioritize retaining other more frequently used and important phone numbers. Over time, Jenny's number may be pruned and gradually forgotten due to its lower importance and relevance compared to other numbers we use more frequently.
Pruning as a Post-Training Optimization Step: If we apply pruning as a post-training optimization step (your brain has cooked enough, shut it off), it means we have already stored Jenny's number and other phone numbers in our memory, and we are now reevaluating and fine-tuning the importance of each number based on pruning criteria. Doing it this way will have allowed your brain to process how you’ve used the number more precisely, as in, temporally. A really big burst of use in the 80s? Great let’s keep it. But wait, it never got used again? “To the brain trash!”, we can assert rather confidently.
In all these scenarios, pruning our brains at different times would likely lead to different outcomes for our memory of Jenny's number. Whether we never store it in the first place, gradually forget it during the learning process, or intentionally remove it as part of post-training optimization, pruning plays a crucial role in shaping what information we retain and prioritize in our memory.
Wow, you’ve made it quite far if you’re still reading. Nice work! Here’s a short poem before continuing:
Roses are red
Violets are blue
For the nth time,
stop calling hard drives CPUs.
I promise, you are not far from the end now.
Should I Prune My Neural Network?
The answer is probably yes given that all models can stand to be optimized in some way. However, here are some specific scenarios when you should consider pruning your neural network:
You need to deploy your neural network on resource-constrained devices or environments.
You’re looking to make a real-time or low-latency application.
You have a model, but need it to improve it generalization ability.
You want to transfer a pre-trained neural network to another task or domain.
What Do I Use to Prune?
There are more than two, but PyTorch and TensorFlow are used to prune a wide array of different models. To do the same using either of these frameworks, you can follow these general steps:
1. Define and train your model: Build and train your neural network model using PyTorch or TensorFlow as you normally would on your specific task and dataset.
2. Implement the pruning technique: There are various pruning techniques available. You can choose from weight pruning, neuron pruning, or other structured pruning methods. Implement the pruning mechanism in your model based on your chosen technique.
For PyTorch:
4. Use PyTorch pruning functions: PyTorch provides built-in functions for pruning. You can use the torch.nn.utils.prune module to add pruning to your model. This module offers options for both weight pruning and neuron pruning. You can specify the pruning criterion (e.g., L1 norm, L2 norm) and the pruning ratio to achieve the desired level of sparsity.
For TensorFlow:
4. Use TensorFlow pruning functions: TensorFlow provides various pruning options through its tf.keras.layers module. You can use the built-in pruning layers like tf.keras.layers.Pruning to apply pruning to your model. You can set the pruning method (e.g., L1 norm, L2 norm) and the pruning ratio to control the sparsity level.
Remember that the process of pruning can be sensitive and might require hyperparameter tuning to strike the right balance between sparsity and performance. Experiment with different pruning ratios, methods, and fine-tuning strategies to find the best configuration for your specific use case. Make sure to consult the official documentation and examples for PyTorch and TensorFlow for more detailed guidance on how to implement pruning for your models.
For some of the more complex pruning methods discussed in this post, neither TensorFlow nor PyTorch have built-in capabilities for. However, PyTorch has left torch.nn.utils.prune fairly flexible so that you may extend it with your own custom pruning function. You can learn more about how to do that here. Similarly, TensorFlow has a lot of customizability options- in fact, they’ve created a comprehensive guide to how to prune more personally here.
This All Sounds Great. What’s the Catch?
It IS great! Deep model pruning offers several advantages beyond model compression. It can enable faster inference times, making it especially beneficial for applications with real-time constraints. Additionally, it reduces the memory footprint, which is advantageous for deployment on resource-constrained devices like embedded systems. Moreover, smaller models require fewer computational resources, resulting in reduced energy consumption and cost savings.
However, as with any good thing, there are some considerations to keep in mind. Pruning can lead to a loss of information, and finding the right balance between sparsity and performance is crucial. Fine-tuning after pruning can be computationally expensive and may require additional data. Selecting the proper pruning criteria and ratio significantly affects the model's final performance. Achieving high sparsity might necessitate iterative pruning, adding to the overall complexity. Additionally, hardware support for sparse computations and transfer learning challenges must be considered.
In general, it requires additional computational overhead to analyze and evaluate neuron activations, especially in larger networks. Furthermore, even upon success with sparsity, sparsity can lead to even more challenges in machine learning models. Arushi Prakash, in his article “Working With Sparse Features In Machine Learning Models” describes some of the most prevalent, which I will relay here: When dealing with many sparse features, the complexity of the models increases in terms of space and time. Linear regression models will need to fit more coefficients, while tree-based models will have deeper trees to account for all the features. Additionally, the behavior of model algorithms and diagnostic measures may become unpredictable when working with sparse data. Goodness-of-fit tests, for instance, may not work well in such cases, as shown by Kuss (2002). Having an excessive number of features can also result in overfitting, where models start fitting noise in the training data instead of learning meaningful patterns. This overfitting makes the models perform poorly when exposed to new data during production, reducing their predictive power.
Another issue Prakash points out is that certain models might underestimate the importance of sparse features and give more preference to denser features, even if the sparse features hold predictive power. For example, tree-based models like random forests may overpredict the importance of features with more categories compared to those with fewer categories. This behavior can skew the model's decision-making process and compromise the accuracy of predictions. Not to mention that most frameworks and hardware cannot accelerate sparse matrices’ computation, meaning that no matter how many zeros you fill the parameter tensors with, it will not impact the actual cost of the network.
Despite these challenges, deep model pruning remains a powerful technique for creating efficient and high-performing neural networks when implemented thoughtfully. ♫ 867-5309 ♪ Did you sing it? Another reason not to worry; pruning is not your only path forward to forgetting Jenny’s phone number. Let’s chat about distillation. But don’t worry, not now. This post is long enough, so our distillation and quantization chats are going to be a separate post. So, too-da-loo for now.
It was shown that large-sparse models often outperform small-dense models across various different architectures.
There are two main reasons for using a low learning rate during fine-tuning:
Avoiding Catastrophic Forgetting: Fine-tuning involves updating the weights of the later layers to accommodate the new task or dataset. However, if the learning rate is set too high, the model might undergo significant changes in the later layers, causing it to "forget" the previously learned representations from the pre-training phase. This phenomenon is known as catastrophic forgetting, and it can lead to a substantial drop in performance on the original task for which the model was pre-trained. Using a low learning rate helps to mitigate this issue by making gradual and incremental updates to the later layers, allowing the model to retain its previously learned knowledge.
Stabilizing Training: A low learning rate ensures more stable and controlled updates to the model's weights during fine-tuning. Since the earlier layers of the pre-trained model have already learned valuable features, they are usually closer to optimal weights for general feature extraction. By fine-tuning with a low learning rate, the model can make fine adjustments to the later layers without drastically altering the well-learned initial representations. This stabilizes the training process and helps the model converge to a good solution for the new task without significantly disrupting the existing knowledge.